BFS vs DFS – Difference Between Them

What is BFS?

BFS is an algorithm that is used to graph data or searching tree or traversing structures. The algorithm efficiently visits and marks all the key nodes in a graph in an accurate breadthwise fashion.

This algorithm selects a single node (initial or source point) in a graph and then visits all the nodes adjacent to the selected node. Once the algorithm visits and marks the starting node, then it moves towards the nearest unvisited nodes and analyses them.

Once visited, all nodes are marked. These iterations continue until all the nodes of the graph have been successfully visited and marked. The full form of BFS is the Breadth-first search.

What is DFS?

DFS is an algorithm for finding or traversing graphs or trees in depth-ward direction. The execution of the algorithm begins at the root node and explores each branch before backtracking. It uses a stack data structure to remember, to get the subsequent vertex, and to start a search, whenever a dead-end appears in any iteration. The full form of DFS is Depth-first search.

Difference between BFS and DFS Binary Tree

Here are the important differences between BFS and DFS.

BFS	DFS
BFS finds the shortest path to the destination.	DFS goes to the bottom of a subtree, then backtracks.
The full form of BFS is Breadth-First Search.	The full form of DFS is Depth First Search.
It uses a queue to keep track of the next location to visit.	It uses a stack to keep track of the next location to visit.
BFS traverses according to tree level.	DFS traverses according to tree depth.
It is implemented using FIFO list.	It is implemented using LIFO list.
It requires more memory as compare to DFS.	It requires less memory as compare to BFS.
This algorithm gives the shallowest path solution.	This algorithm doesn’t guarantee the shallowest path solution.
There is no need of backtracking in BFS.	There is a need of backtracking in DFS.
You can never be trapped into finite loops.	You can be trapped into infinite loops.
If you do not find any goal, you may need to expand many nodes before the solution is found.	If you do not find any goal, the leaf node backtracking may occur.

Example of BFS

In the following example of BFS, we have used graph having 6 vertices.

Example of BFS

Step 1)

You have a graph of seven numbers ranging from 0 – 6.

Step 2)

0 or zero has been marked as a root node.

Step 3)

0 is visited, marked, and inserted into the queue data structure.

Step 4)

Remaining 0 adjacent and unvisited nodes are visited, marked, and inserted into the queue.

Step 5)

Traversing iterations are repeated until all nodes are visited.

Example of DFS

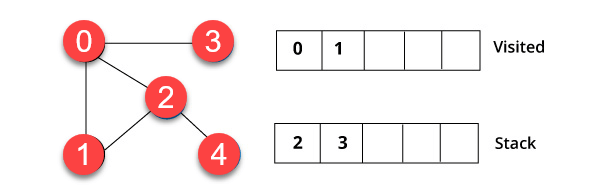
In the following example of DFS, we have used an undirected graph having 5 vertices.

Step 1)

We have started from vertex 0. The algorithm begins by putting it in the visited list and simultaneously putting all its adjacent vertices in the data structure called stack.

Step 2)

You will visit the element, which is at the top of the stack, for example, 1 and go to its adjacent nodes. It is because 0 has already been visited. Therefore, we visit vertex 2.

Step 3)

Vertex 2 has an unvisited nearby vertex in 4. Therefore, we add that in the stack and visit it.

Step 4)

Finally, we will visit the last vertex 3, it doesn’t have any unvisited adjoining nodes. We have completed the traversal of the graph using DFS algorithm.

Applications of BFS

Here, are Applications of BFS:

Un-weighted Graphs

BFS algorithm can easily create the shortest path and a minimum spanning tree to visit all the vertices of the graph in the shortest time possible with high accuracy.

P2P Networks

BFS can be implemented to locate all the nearest or neighboring nodes in a peer to peer network. This will find the required data faster.

Web Crawlers

Search engines or web crawlers can easily build multiple levels of indexes by employing BFS. BFS implementation starts from the source, which is the web page, and then it visits all the links from that source.

Network Broadcasting

A broadcasted packet is guided by the BFS algorithm to find and reach all the nodes it has the address for.

Applications of DFS

Here are Important applications of DFS:

Weighted Graph

In a weighted graph, DFS graph traversal generates the shortest path tree and minimum spanning tree.

Detecting a Cycle in a Graph

A graph has a cycle if we found a back edge during DFS. Therefore, we should run DFS for the graph and verify for back edges.

Path Finding

We can specialize in the DFS algorithm to search a path between two vertices.

Topological Sorting

It is primarily used for scheduling jobs from the given dependencies among the group of jobs. In computer science, it is used in instruction scheduling, data serialization, logic synthesis, determining the order of compilation tasks.

Searching Strongly Connected Components of a Graph

It used in DFS graph when there is a path from each and every vertex in the graph to other remaining vertexes.

Solving Puzzles with Only One Solution

DFS algorithm can be easily adapted to search all solutions to a maze by including nodes on the existing path in the visited set.