Breadth First Search (BFS) Algorithm with EXAMPLE
What is BFS Algorithm (Breadth-First Search)?
Breadth-first search (BFS) is an algorithm that is used to graph data or searching tree or traversing structures. The full form of BFS is the Breadth-first search.
The algorithm efficiently visits and marks all the key nodes in a graph in an accurate breadthwise fashion. This algorithm selects a single node (initial or source point) in a graph and then visits all the nodes adjacent to the selected node. Remember, BFS accesses these nodes one by one.
Once the algorithm visits and marks the starting node, then it moves towards the nearest unvisited nodes and analyses them. Once visited, all nodes are marked. These iterations continue until all the nodes of the graph have been successfully visited and marked.
What is Graph traversals?
A graph traversal is a commonly used methodology for locating the vertex position in the graph. It is an advanced search algorithm that can analyze the graph with speed and precision along with marking the sequence of the visited vertices. This process enables you to quickly visit each node in a graph without being locked in an infinite loop.
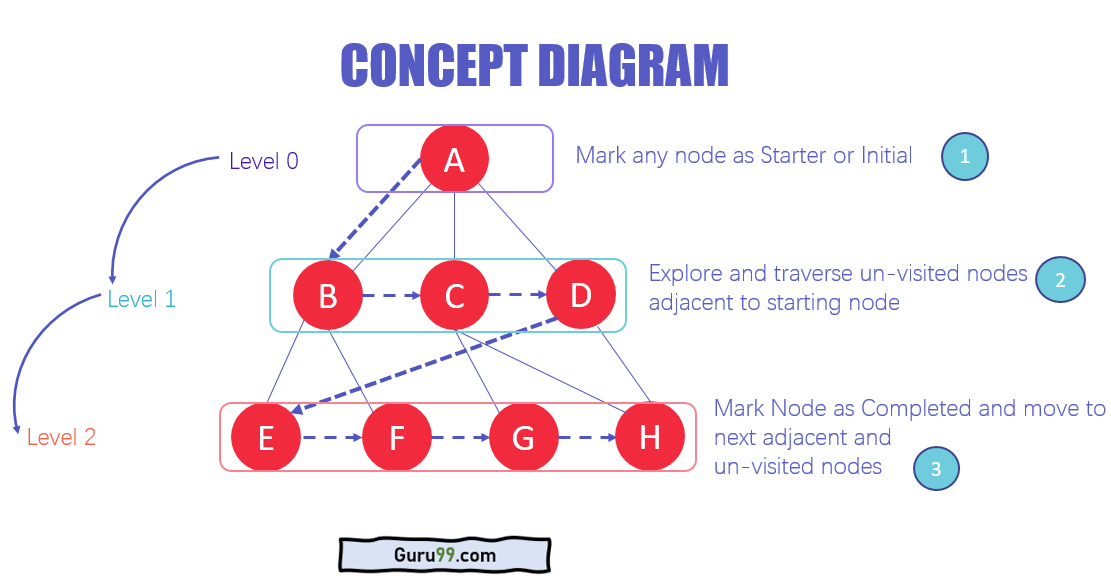
The architecture of BFS algorithm
- In the various levels of the data, you can mark any node as the starting or initial node to begin traversing. The BFS will visit the node and mark it as visited and places it in the queue.
- Now the BFS will visit the nearest and un-visited nodes and marks them. These values are also added to the queue. The queue works on the FIFO model.
- In a similar manner, the remaining nearest and un-visited nodes on the graph are analyzed marked and added to the queue. These items are deleted from the queue as receive and printed as the result.
Why do we need BFS Algorithm?
There are numerous reasons to utilize the BFS Algorithm to use as searching for your dataset. Some of the most vital aspects that make this algorithm your first choice are:
- BFS is useful for analyzing the nodes in a graph and constructing the shortest path of traversing through these.
- BFS can traverse through a graph in the smallest number of iterations.
- The architecture of the BFS algorithm is simple and robust.
- The result of the BFS algorithm holds a high level of accuracy in comparison to other algorithms.
- BFS iterations are seamless, and there is no possibility of this algorithm getting caught up in an infinite loop problem.
How does BFS Algorithm Work?
Graph traversal requires the algorithm to visit, check, and/or update every single un-visited node in a tree-like structure. Graph traversals are categorized by the order in which they visit the nodes on the graph.
BFS algorithm starts the operation from the first or starting node in a graph and traverses it thoroughly. Once it successfully traverses the initial node, then the next non-traversed vertex in the graph is visited and marked.
Hence, you can say that all the nodes adjacent to the current vertex are visited and traversed in the first iteration. A simple queue methodology is utilized to implement the working of a BFS algorithm, and it consists of the following steps:
Step 1)
Each vertex or node in the graph is known. For instance, you can mark the node as V.
Step 2)
In case the vertex V is not accessed then add the vertex V into the BFS Queue
Step 3)
Start the BFS search, and after completion, Mark vertex V as visited.
Step 4)
The BFS queue is still not empty, hence remove the vertex V of the graph from the queue.
Step 5)
Retrieve all the remaining vertices on the graph that are adjacent to the vertex V
Step 6)
For each adjacent vertex let’s say V1, in case it is not visited yet then add V1 to the BFS queue
Step 7)
BFS will visit V1 and mark it as visited and delete it from the queue.
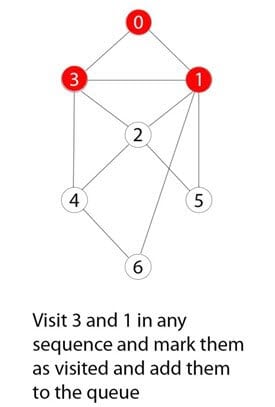
Example BFS Algorithm
Step 1)
You have a graph of seven numbers ranging from 0 – 6.
Step 2)
0 or zero has been marked as a root node.
Step 3)
0 is visited, marked, and inserted into the queue data structure.
Step 4)
Remaining 0 adjacent and unvisited nodes are visited, marked, and inserted into the queue.
Step 5)
Traversing iterations are repeated until all nodes are visited.
Rules of BFS Algorithm
Here, are important rules for using BFS algorithm:
- A queue (FIFO-First in First Out) data structure is used by BFS.
- You mark any node in the graph as root and start traversing the data from it.
- BFS traverses all the nodes in the graph and keeps dropping them as completed.
- BFS visits an adjacent unvisited node, marks it as done, and inserts it into a queue.
- Removes the previous vertex from the queue in case no adjacent vertex is found.
- BFS algorithm iterates until all the vertices in the graph are successfully traversed and marked as completed.
- There are no loops caused by BFS during the traversing of data from any node.
Applications of BFS Algorithm
Let’s take a look at some of the real-life applications where a BFS algorithm implementation can be highly effective.
- Un-weighted Graphs: BFS algorithm can easily create the shortest path and a minimum spanning tree to visit all the vertices of the graph in the shortest time possible with high accuracy.
- P2P Networks: BFS can be implemented to locate all the nearest or neighboring nodes in a peer to peer network. This will find the required data faster.
- Web Crawlers: Search engines or web crawlers can easily build multiple levels of indexes by employing BFS. BFS implementation starts from the source, which is the web page, and then it visits all the links from that source.
- Navigation Systems: BFS can help find all the neighboring locations from the main or source location.
- Network Broadcasting: A broadcasted packet is guided by the BFS algorithm to find and reach all the nodes it has the address for.
Summary
- A graph traversal is a unique process that requires the algorithm to visit, check, and/or update every single un-visited node in a tree-like structure. BFS algorithm works on a similar principle.
- The algorithm is useful for analyzing the nodes in a graph and constructing the shortest path of traversing through these.
- The algorithm traverses the graph in the smallest number of iterations and the shortest possible time.
- BFS selects a single node (initial or source point) in a graph and then visits all the nodes adjacent to the selected node. BFS accesses these nodes one by one.
- The visited and marked data is placed in a queue by BFS. A queue works on a first in first out basis. Hence, the element placed in the graph first is deleted first and printed as a result.
- The BFS algorithm can never get caught in an infinite loop.
- Due to high precision and robust implementation, BFS is used in multiple real-life solutions like P2P networks, Web Crawlers, and Network Broadcasting.