Knapsack Problem: Dynamic Programming Example

Details

What is the Knapsack Problem?

In the supermarket there are n packages (n ≤ 100) the package i has weight W[i] ≤ 100 and value V[i] ≤ 100. A thief breaks into the supermarket, the thief cannot carry weight exceeding M (M ≤ 100). The problem to be solved here is: which packages the thief will take away to get the highest value?

Input:

  • Maximum weight M and the number of packages n.
  • Array of weight W[i] and corresponding value V[i].

Output:

  • Maximize value and corresponding weight in capacity.
  • Which packages the thief will take away.

Knapsack problem can be further divided into two types:

  • The 0/1 Knapsack Problem. In this type, each package can be taken or not taken. Besides, the thief cannot take a fractional amount of a taken package or take a package more than once. This type can be solved by Dynamic Programming Approach.
  • Fractional Knapsack Problem. This type can be solved by Greedy Strategy.

In this tutorial, you will learn:

Brief Introduction of Dynamic Programming

In the divide-and-conquer strategy, you divide the problem to be solved into subproblems. The subproblems are further divided into smaller subproblems. That task will continue until you get subproblems that can be solved easily. However, in the process of such division, you may encounter the same problem many times.

The basic idea of dynamic programming is to use a table to store the solutions of solved subproblems. If you face a subproblem again, you just need to take the solution in the table without having to solve it again. Therefore, the algorithms designed by dynamic programming are very effective.

To solve a problem by dynamic programming, you need to do the following tasks:

  • Find solutions of the smallest subproblems.
  • Find out the formula (or rule) to build a solution of subproblem through solutions of even smallest subproblems.
  • Create a table that stores the solutions of subproblems. Then calculate the solution of subproblem according to the found formula and save to the table.
  • From the solved subproblems, you find the solution of the original problem.

Analyze the 0/1 Knapsack Problem

When analyzing this type, you can find some noticeable points. The value of the knapsack algorithm depends on two factors:

  1. How many packages are being considered
  2. The remaining weight which the knapsack can store.

Therefore, you have two variable quantities.

With dynamic programming, you have useful information:

  1. the objective function will depend on two variable quantities
  2. the table of options will be a 2-dimensional table.

If calling B[i][j] is the maximum possible value by selecting in packages {1, 2, ..., i} with weight limit j.

  • The maximum value when selected in n packages with the weight limit M is B[n][M]. In other words: When there are i packages to choose, B[i][j] is the optimal weight when the maximum weight of the knapsack is j.
  • The optimal weight is always less than or equal to the maximum weight: B[i][j] ≤ j.

For example: B[4][10] = 8. It means that in the optimal case, the total weight of the selected packages is 8, when there are 4 first packages to choose from (1st to 4th package) and the maximum weight of the knapsack is 10. It is not necessary that all 4 items are selected.

Formula to Calculate B[i][j]

Input, you define:

  • W[i], V[i] are in turn the weight and value of package i, in which i {1, …, n}.
  • M is the maximum weight that the knapsack can carry.

In the case of simply having only 1 package to choose. You calculate B[1][j] for every j: which means the maximum weight of the knapsack ≥ the weight of the 1st package 

B[1][j] = W[1]

With the weight limit j, the optimal selections among packages {1, 2, ..., i – 1, i} to have the largest value will have two possibilities:

  • If package i is not selected, B[i][j] is the maximum possible value by selecting among packages {1, 2, ..., i – 1} with weight limit of j. You have:
B[i][j] = B[i – 1][j]
  • If package i is selected (of course only consider this case when W[i] ≤ j) then B[i][j] is equal to the value V[i] of package i plus the maximum value can be obtained by selecting among packages {1, 2, ..., i – 1} with weight limit (j – W[i]). That is, in terms of the value you have:
B[i][j] = V[i] + B[i – 1][j – W[i]]

Due to the creation of B[i][j], which is the maximum possible value, B[i][j] will be the max of the above 2 values.

Basis of Dynamic Programming

So, you have to consider if it is better to choose package i or not. From there you have the recursive formula as follows: 

B[i][j]= max(B[i – 1][j], V[i]+B[i – 1][j – W[i]]

It is easy to see B[0][j] = maximum value possible by selecting from 0 package = 0.

Calculate the Table of Options

You build a table of options based on the above recursive formula. To check if the results are correct (if not exactly, you rebuild the objective function B[i][j]). Through the creation of the objective function B[i][j] and the table of options, you will orient the tracing.

Table of options B includes n + 1 lines, M + 1 columns,

  • Firstly, filled with the basis of dynamic programming: Line 0 includes all zeros.
  • Using recursive formulas, use line 0 to calculate line 1, use line 1 to calculate line 2, etc. ... until all lines are calculated.
Table of Options

Trace

When calculating the table of options, you are interested in B[n][M] which is the maximum value obtained when selecting in all n packages with the weight limit M.

  • If B[n][M] = B[n – 1][M] then package n is not selected, you trace B[n – 1][M].
  • If B[n][M] ≠ B[n – 1][M], you notice that the optimal selection has the package n and trace B[n – 1][M – W[n]].

Continue to trace until reaching row 0 of the table of options.

Algorithm to Look Up the Table of Options to Find the Selected Packages

Note: If B[i][j] = B[i – 1][j], the package i is not selected. B[n][W] is the optimal total value of package put into the knapsack.

Steps for tracing:

  • Step 1: Starting from i = n, j = M.
  • Step 2: Look in column j, up from bottom, you find the line i such that B[i][j] > B[i – 1][j]. Mark selected package i: Select [i] = true;
  • Step 3: j = B[i][j] – W[i]. If j > 0, go to step 2, otherwise go to step 4
  • Step 4: Based on the table of options to print the selected packages.

Java Code

public void knapsackDyProg(int W[], int V[], int M, int n) {
	int B[][] = new int[n + 1][M + 1];
	
	for (int i=0; i<=n; i++)
		for (int j=0; j<=M; j++) {
			B[i][j] = 0;
		}
	
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= M; j++) {
			B[i][j] = B[i - 1][j];
			
			if ((j >= W[i-1]) && (B[i][j] < B[i - 1][j - W[i - 1]] + V[i - 1])) {
				B[i][j] = B[i - 1][j - W[i - 1]] + V[i - 1]; 
			}
			
			System.out.print(B[i][j] + " ");
		}
		System.out.print("\n");
	}
	
	System.out.println("Max Value:\t" + B[n][M]);
	
	System.out.println("Selected Packs: ");
	
	while (n != 0) {
		if (B[n][M] != B[n - 1][M]) {
			System.out.println("\tPackage " + n + " with W = " + W[n - 1] + " and Value = " + V[n - 1]);
			
			M = M - W[n-1];
		}
		
		n--;
	}
}
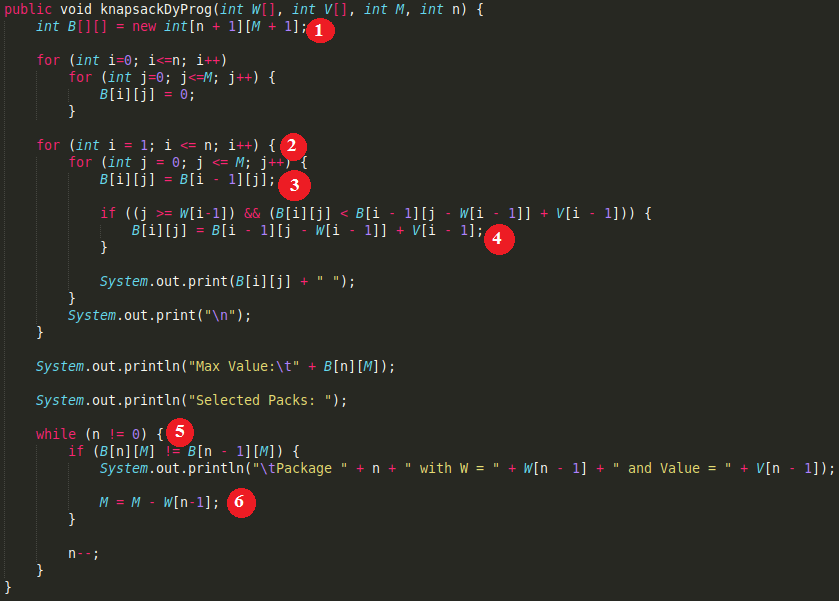
Function knapsackDyProg() in Java

Explanation of code:

  1. Create table B[][]. Set default value for each cell is 0.
  2. Build table B[][] in bottom-up manner. Calculate the table of options with the retrieval formula.
  3. Calculate B[i][j]. If you do not select package i.
  4. Then evaluate: if you select package i, it will be more beneficial then reset B[i][j].
  5. Trace the table from row n to row 0.
  6. If you choose package n. Once select package n, can only add weight M - W[n - 1].

In this tutorial, you have two examples. Here is java code to run the above program with two examples: 

public void run() {
	/*
	 * Pack and Weight - Value
	 */
	//int W[] = new int[]{3, 4, 5, 9, 4};
	int W[] = new int[]{12, 2, 1, 1, 4};
	
	//int V[] = new int[]{3, 4, 4, 10, 4};
	int V[] = new int[]{4, 2, 1, 2, 10};
	
	/*
	 * Max Weight
	 */
	//int M = 11;
	int M = 15;
	int n = V.length;
	
	/*
	 * Run the algorithm
	 */
	knapsackDyProg(W, V, M, n);
}

You have the output:

  • First Example:
0 0 0 3 3 3 3 3 3 3 3 3 
0 0 0 3 4 4 4 7 7 7 7 7 
0 0 0 3 4 4 4 7 7 8 8 8 
0 0 0 3 4 4 4 7 7 10 10 10 
0 0 0 3 4 4 4 7 8 10 10 11 
Max Value:	11
Selected Packs: 
	Package 5 with W = 4 and Value = 4
	Package 2 with W = 4 and Value = 4
	Package 1 with W = 3 and Value = 3
  • Second Example:
0 0 0 0 0 0 0 0 0 0 0 0 4 4 4 4 
0 0 2 2 2 2 2 2 2 2 2 2 4 4 6 6 
0 1 2 3 3 3 3 3 3 3 3 3 4 5 6 7 
0 2 3 4 5 5 5 5 5 5 5 5 5 6 7 8 
0 2 3 4 10 12 13 14 15 15 15 15 15 15 15 15
Max Value:	15
Selected Packs: 
	Package 5 with W = 4 and Value = 10
	Package 4 with W = 1 and Value = 2
	Package 3 with W = 1 and Value = 1
	Package 2 with W = 2 and Value = 2

 

YOU MIGHT LIKE: